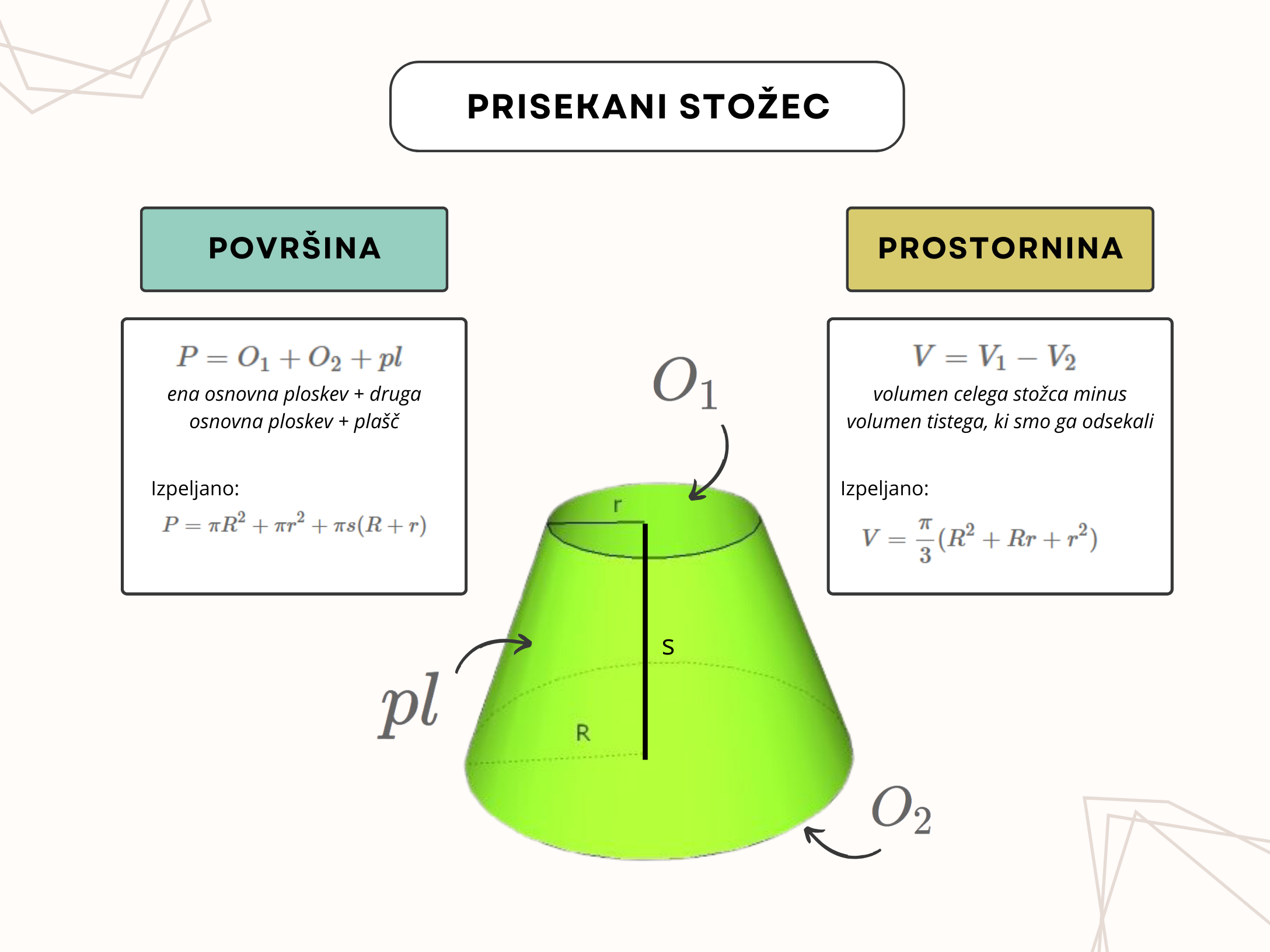
PROSTORNINA PRISEKANEGA STOŽCA

Izpeljimo obrazec za prostornino prisekanega stožca. Pri tem si pomagajmo tudi z naslednjo sliko:

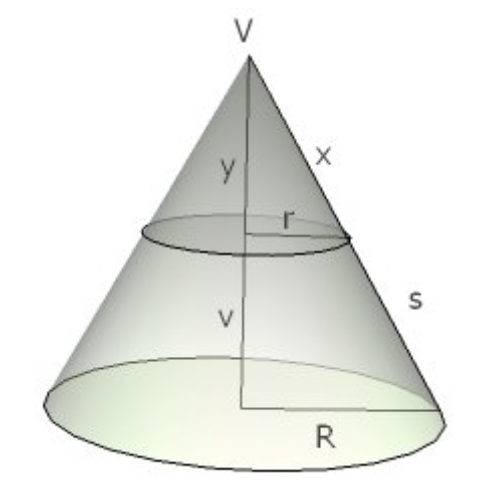
Prostornina prisekanega stožca je enaka razliki prostornin osnovnega in prisekanega stožca:

\[V=V_1-V_2\]

\(V_1\) predstavlja prostornino osnovnega stožca \(R\). \(V_2\) pa predstavlja prostornino prisekanega stožca.

\[V=\frac{\pi (v+y)R^2}{3} – \frac{\pi yr^2}{3}\]

Za lažjo izpeljavo enačbe izpostavimo \(\frac{\pi}{3}\).

\[V=\frac{\pi}{3}(vR^2+yR^2-yr^2)\]

V enačbi se je potrebno znebiti neznanke \(y\), zato jo izpostavimo.

\[V=\frac{\pi}{3}(vR^2+y(R^2-r^2)\]

Za odpravljanje spremenljivke \(y\) bomo uporabili izrek o podobnih trikotnikih, saj imamo v stožcu dva podobna trikotanika. Torej trikotnika sta podobna, če se ujemata v dveh razmerjih istoležečih stranic. Tako dobimo

\[y:r=(y+v):R\]

ki ga preoblikujemo tako, da izrazimo spremenljivko \(y\). V naši enačbi zamenjamo izraženo spremenljivko

\[y=\frac{rv}{R-r}\]

Nato vstavimo

\[V=\frac{\pi}{3}(vR^2+\frac{rv}{R-r}(R^2-r^2))\]

V dobljeni enačbi razstavimo razliko kvadratov \(R^2-r^2 = (R-r)(R+r)\) ter okrajšamo ulomek.

\[V=\frac{\pi}{3}(vR^2+rv(R+r))\]

Odpravimo oklepaje.

\[V=\frac{\pi vR^2}{3}+\frac{\pi vRr}{3}+\frac{\pi vr^2}{3}\]

Iz nastale enačbe izpostavimo skupni faktor \(\frac{\pi v}{3}\) in dobimo enačbo za prostornino prisekanega stožca.

\[V=\frac{\pi}{3}(R^2+Rr+r^2)\]

NALOGA ZA UTRJEVANJE

Koliko peska lahko natrosimo v posodico oblike pokončnega prisekanega stožca s polmeroma R = 26 cm in r = 12 cm ter stranico s = 60 cm?