PITAGOROV IZREK V PRAVILNI 3 – STRANI PIRAMIDI

 

Osnovna ploskev pravilne 3-strane piramide je enakostranični trikotnik, plašč pa sestavljajo trije skladni enakokraki trikotniki.

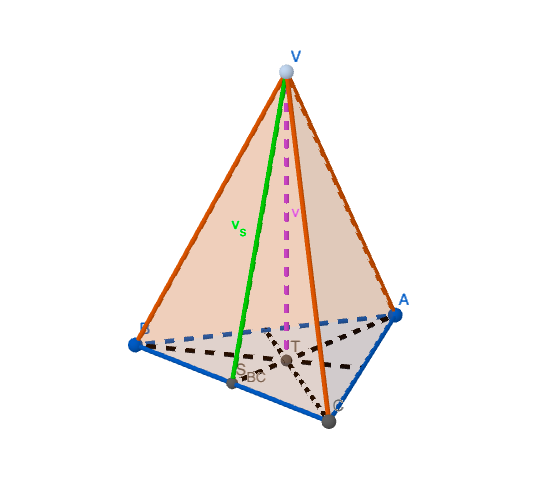
Pravilna 3-strana piramida by Laura R. is licensed under CC BY-NC-SA 4.0

Pravilna 3-strana piramida by Laura R. is licensed under CC BY-NC-SA 4.0

V pravilni 3-strani piramidi opazimo tri različne pravokotne trikotnike, ki so označeni na spodnjih slikah. Z njihovo pomočjo je, podobno kot v pravilni 4-strani piramidi, podana povezava med osnovnim robom a, stranico s, višino v in stransko višino v_s.

\[s^{2}=(\frac{a}{2})^{2}+v_{s}^{2}\]

PI v P3S piramidi by Laura R. is licensed under CC BY-NC-SA 4.0

\[s^{2}=v^{2}+(\frac{a\sqrt3}{3})^{2}\]

PI v P3S piramidi by Laura R. is licensed under CC BY-NC-SA 4.0

\[ v_{s}^{2}=v^{2}+(\frac{a\sqrt3}{6})^{2}\]

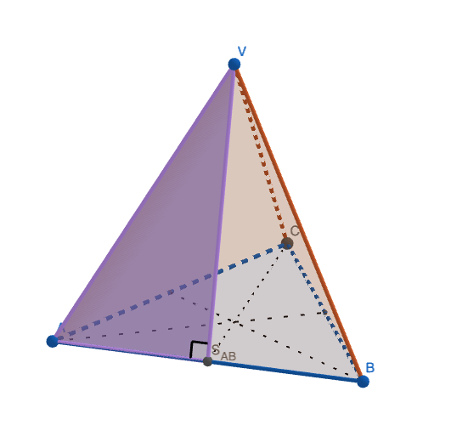
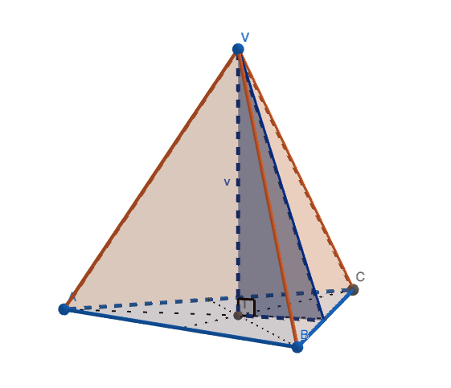
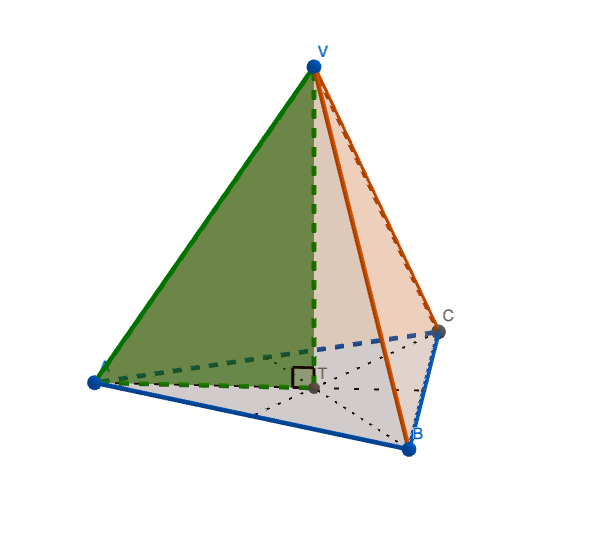
PI v P3S piramidi by Laura R. is licensed under CC BY-NC-SA 4.0

Za razlago in izpeljavo katet pri drugem in tretjem pravokotnem trikotniku si oglej spodnji video.

PI v P3S piramidi by Laura R. is licensed under CC BY-NC-SA 4.0

Prenesi infografiko - PI v P3S piramidi

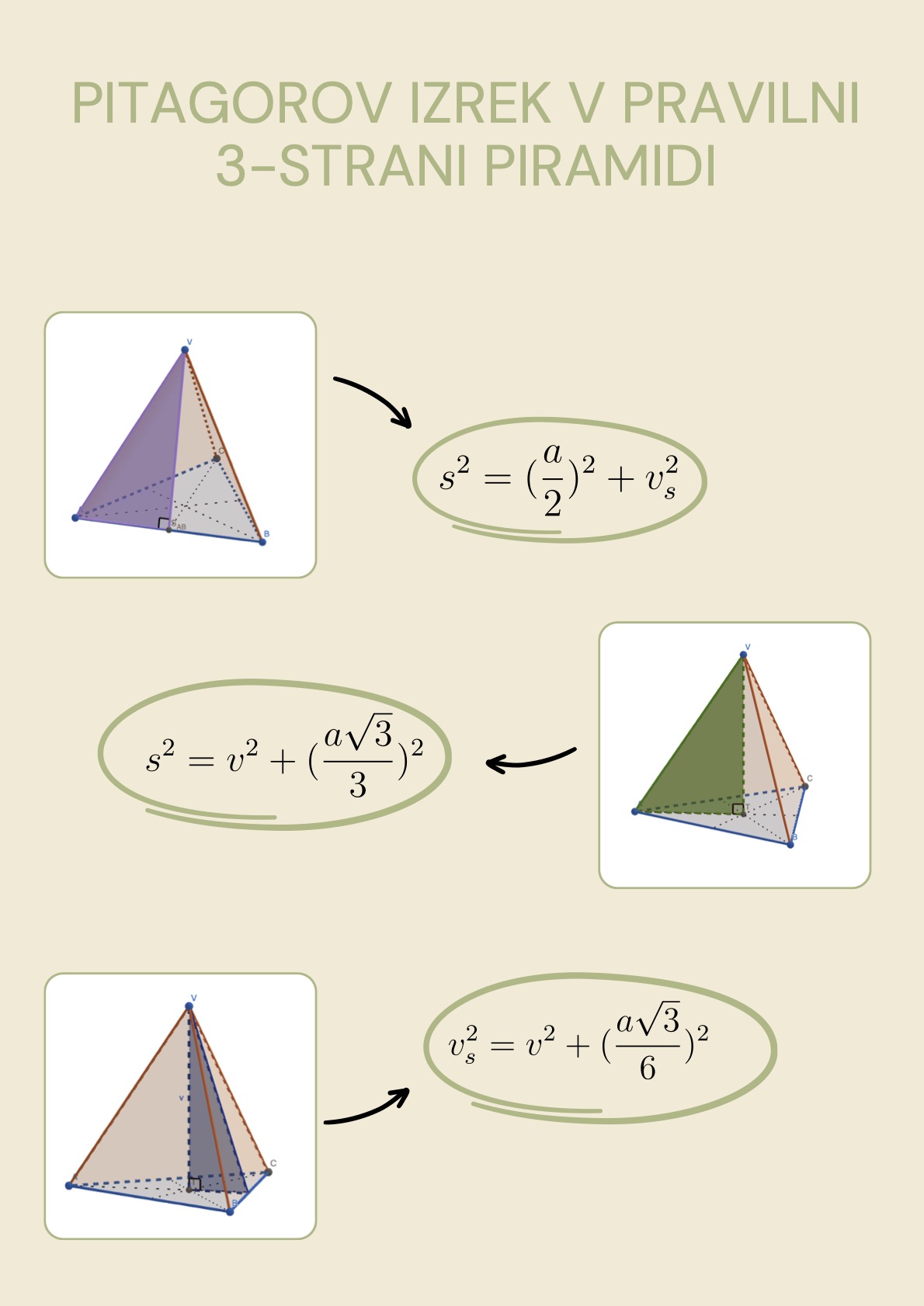
PI v P3S piramidi by Laura R. is licensed under CC BY-NC-SA 4.0

UTRJEVANJE

 

Pitagorov izrek v P3S piramidi - utrjevanje by Laura R. is licensed under CC BY-NC-SA 4.0

Pitagorov izrek v P3S piramidi - utrjevanje poimenovanje by Laura R. is licensed under CC BY-NC-SA 4.0

Pitagorov izrek v P3S piramidi - križanka by Laura R. is licensed under CC BY-NC-SA 4.0