STOŽEC
Definicija
Vrste stožcev
Površina stožca
Prostornina stožca
Naloge
DEFINICIJA
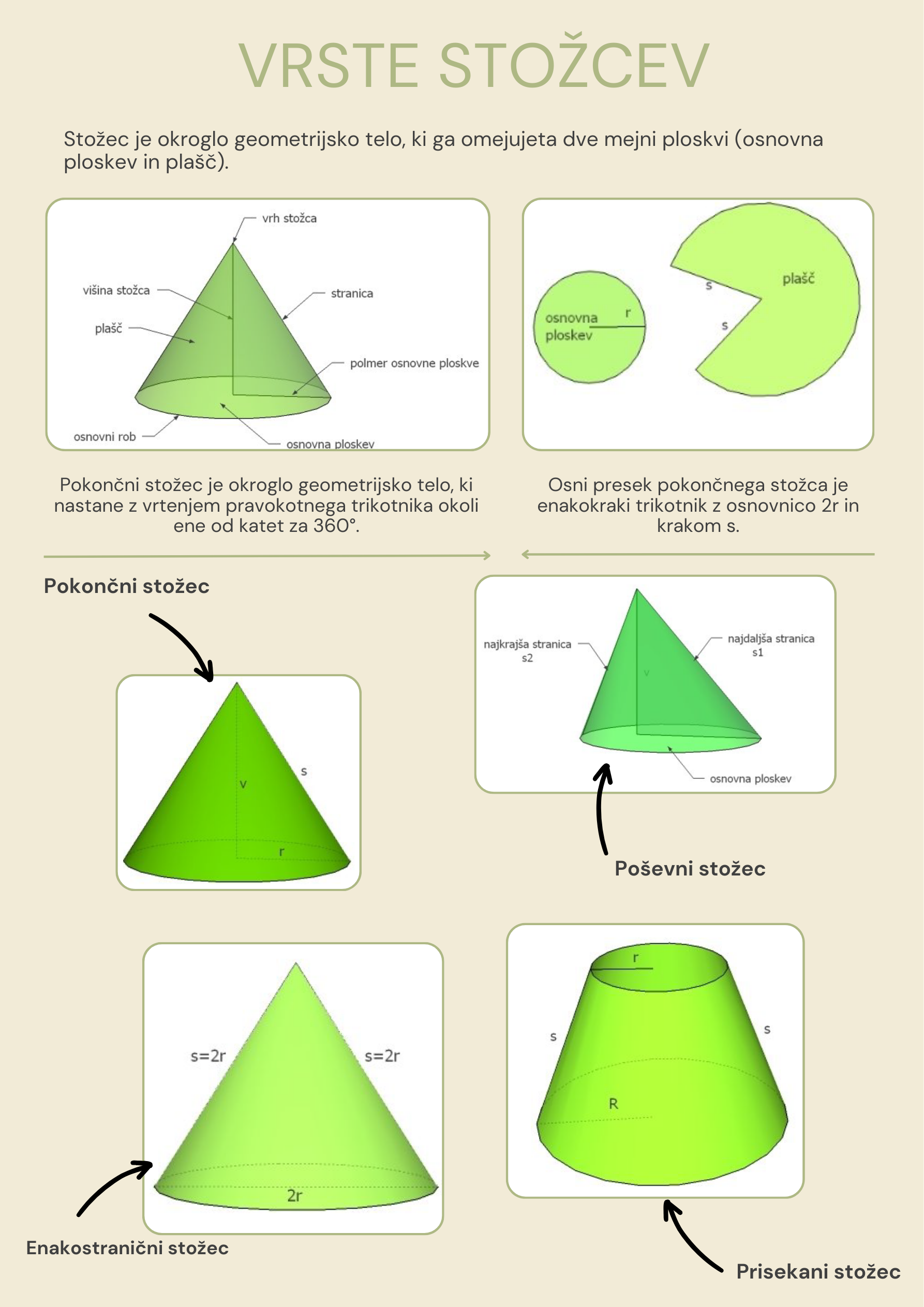
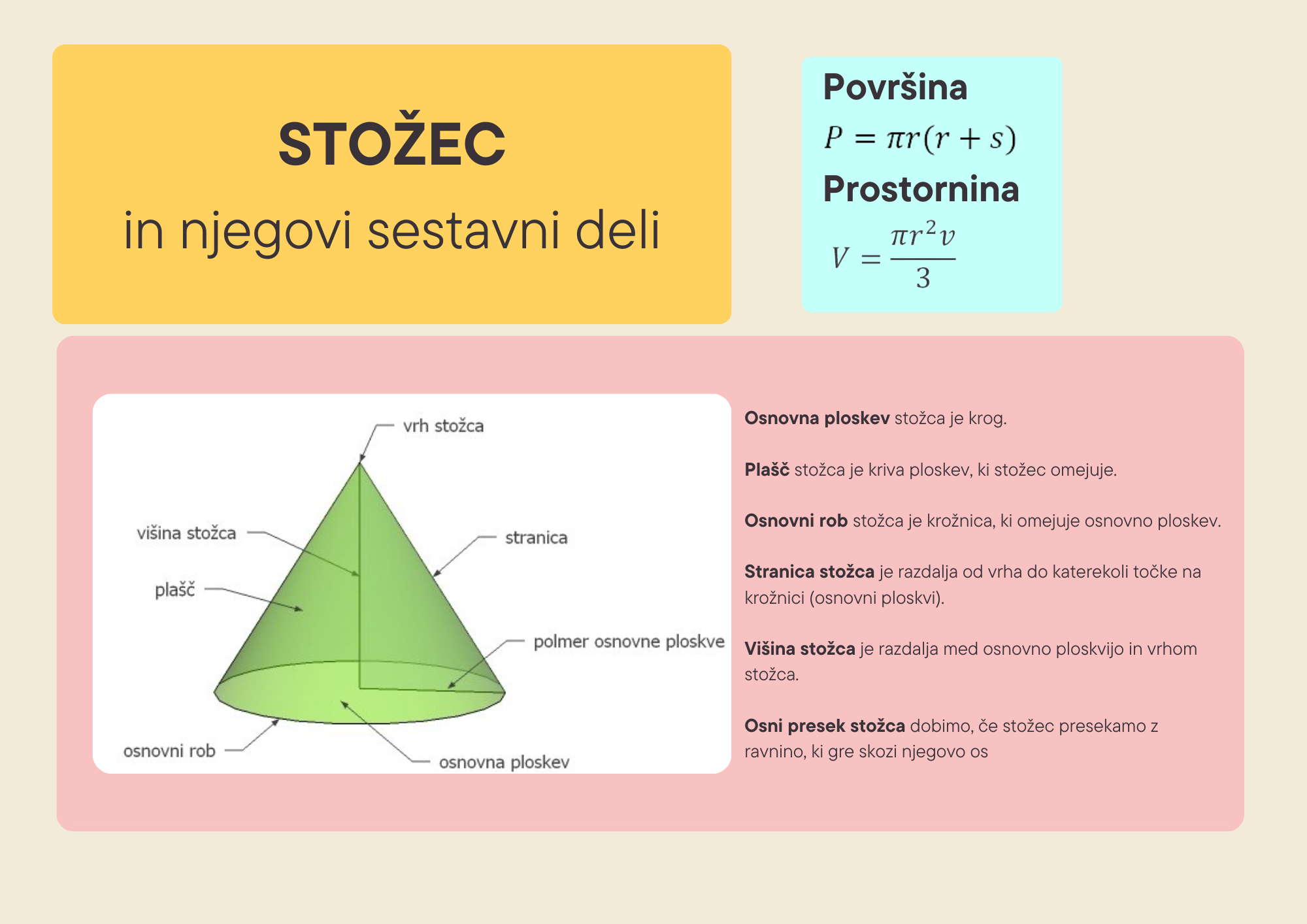
Stožec je okroglo geometrijsko telo, ki ga omejujeta dve mejni ploskvi (osnovna ploskev in plašč).
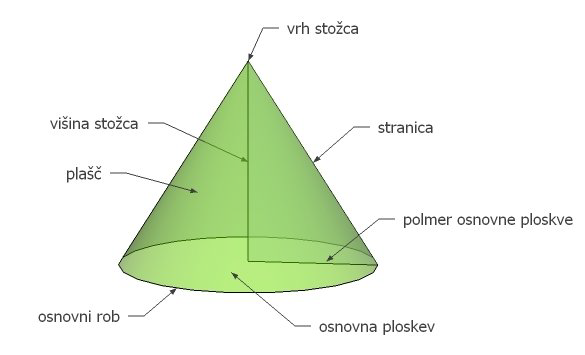
- Osnovna ploskev stožca je krog.
- Plašč stožca je kriva ploskev, ki stožec omejuje.
- Osnovni rob stožca je krožnica, ki omejuje osnovno ploskev.
- Stranica stožca je razdalja od vrha do katerekoli točke na krožnici (osnovni
ploskvi). - Višina stožca je razdalja med osnovno ploskvijo in vrhom stožca.
- Osni presek stožca dobimo, če stožec presekamo z ravnino, ki gre skozi
njegovo os.
VRSTE STOŽCEV
Poznamo pokončne stožce, poševne stožce, enakostranične stožce in prisekane stožce.
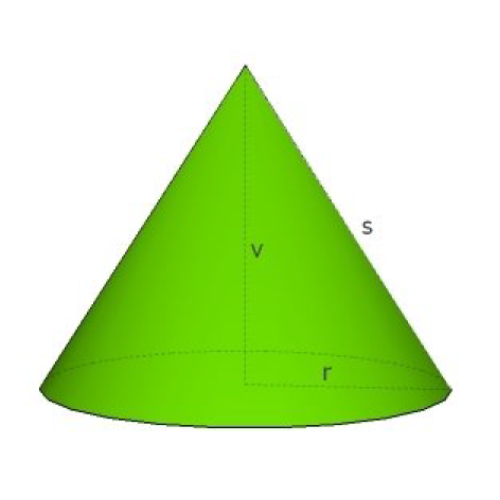
Pokončni stožec
Pokončni stožec je okroglo geometrijsko telo, ki nastane z vrtenjem pravokotnega trikotnika okoli ene od katet za 360◦.
Poševni stožec
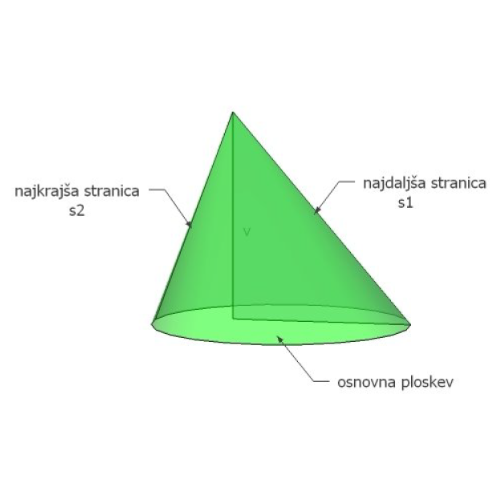
Poševni stožec je okroglo geometrijsko telo, ki ima za osnovno ploskev krog. Os stožca, ki poteka skozi središče in vrh stožca ni pravokotna na osnovno ploskev. Stranice poševnega stožca so različnih dolžin.
Enakostranični stožec
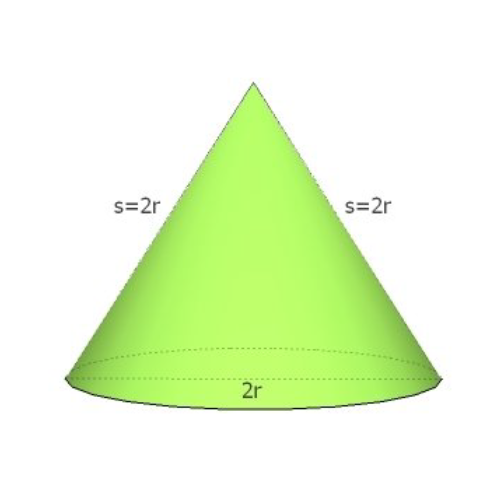
Enakostranični stožec je stožec, ki ima stranice enake premeru osnovne ploskve. Osni presek enakostraničnega stožca je enakostranični trikotnik s stranico 2r.
Prisekani stožec
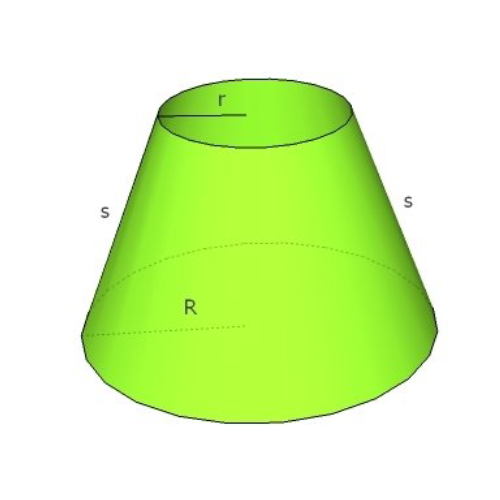
Prisekani stožec dobimo, če stožcu s polmerom R in vrhom V odrežemo vzporedno z osnovno ploskvijo stožec s polmerom r in vrhom V .
Vrste stožcev by Amadej Šuperger is marked with CC0 1.0
POVRŠINA STOŽCA
Površina stožca je vsota ploščin vseh njenih mejnih ploskev (osnovne ploskve in
plašča). Označimo jo s črko P.
Osnovna formula: \[P=O+pl\]
Izpeljana formula: \[P=\pi\cdot r(r+s)\]
PROSTORNINA STOŽCA
Prostornina stožca je enaka tretjini produkta ploščine osnovne ploskve stožca in njegove višine:
Osnovna formula: \[V=\frac{O\cdot v}{3}\]
Izpeljana formula za stožec: \[V=\frac{\pi\cdot r^2 \cdot v}{3}\]
Sestavni deli stožca by Amadej Šuperger is marked with CC0 1.0
NALOGA ZA UTRJEVANJE
Poveži stožec s pravo sliko by Amadej Šuperger is marked with CC0 1.0